Interpolation d'une fonction continue
par la technique des courbes de Bézier
|
La technique peut être employée pour des courbes dont on ne connaît que quelques points caractéristiques. Par exemple, la courbe de la fonction f(x) = sin(x), dont tout bon matheux connaît les valeurs: sin(0) = 0,
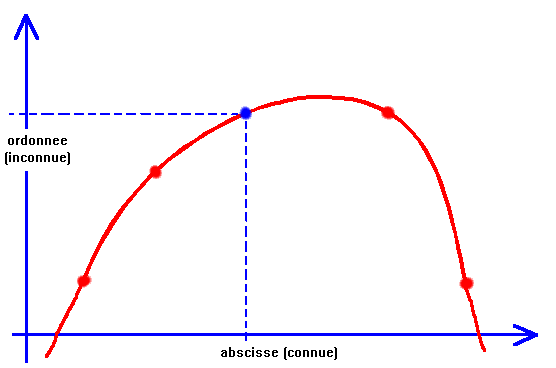
La question que l'on se pose est: comment faire pour calculer approximativement l'ordonnée d'un point situé sur une telle courbe, et dont on connaît l'abscisse? |
.
|
La méthode d'interpolation par courbes de Bézier exige seulement que le point dont on cherche l'ordonnée se trouve à la droite de deux points de la courbe dont on connaît les deux coordonnées, et à la gauche de deux autres points répondant aux mêmes conditions. |
.

|
Avec ces quatre points, on obtient trois segments de droite. |
.

|
On découpe ces segments de droite par tiers, ce qui permet de déterminer les coordonnées de quatre nouveaux points caractéristiques. |
.

|
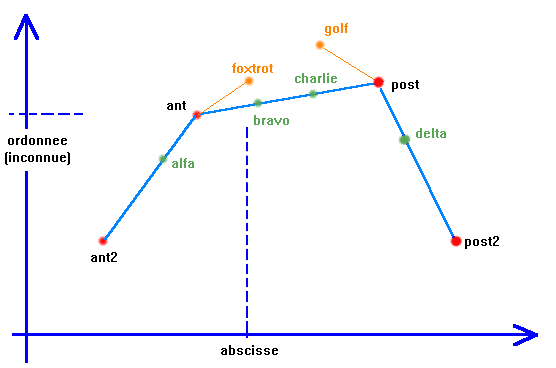
Intéressons-nous maintenant plus particulièrement à la partie du graphique alfa-ant-bravo. Ces deux segments de droite ne sont pas alignés. Pour que la courbe de Bézier que l'on va construire soit continue au point ant, on va déterminer une direction moyenne en calculant un point echo disposé comme sur le schéma ci-dessous. Ensuite, dans l'alignement d'ant et d'echo, on va placer un point foxtrot situé à la même distance d'ant que bravo. |
.

|
D'une façon similaire, on place un point golf à partir des points charlie, post et delta. |
.
|
A l'aide des quatre points ant, foxtrot, golf et post, on calcule un point mike selon le principe des courbes de Bézier. Ce point mike se trouve sur la courbe de Bézier elle-même (c'est le principe même de la construction d'une courbe de Bézier). Nota: pour la lisibilité, on a placé sur le schéma ci-dessous les points ant, foxtrot, golf et post d'une façon qui ne cherche pas à ressembler aux schémas précédents. Mais cela ne change rien à la logique de construction. |
.

|
On admet que ce point mike se trouve aussi sur la courbe mathématique dont on parlait au départ, la courbe de Bézier étant une approximation de cette dernière. |
.

|
Dès lors, il est facile de déterminer si le point dont on recherche l'ordonnée se trouve à gauche ou à droite de mike sur la courbe. |
.

|
Donc, on peut se servir de mike à la place d'un des quatre points de départ (selon les cas, à la place d'ant ou à la place de post). On pourra ainsi, par itération de la même logique, réduire l'intervalle d'incertitude de moitié (à peu près) à chaque itération. Au bout d'un nombre assez réduit d'itérations (environ 32 si l'on stocke les valeurs sur 32 bits), il ne sera plus possible d'exprimer la différence entre l'abscisse du point recherché et celle d'ant, de post ou de mike. On considérera alors que l'on a trouvé l'ordonnée recherchée. . |
Remarque sur le calcul de valeurs irrationnelles
|
La seule partie de cette démarche qui implique des calculs avec des nombres irrationnels est celle concernant le calcul du point foxtrot (calcul trigonométrique traditionnel: l'hypothénuse est la racine carrée de la somme des carrés des deux autres côtés). Toutes les autres opérations sont des divisions par 2 ou par 3. Il est à noter que foxtrot peut être (relativement) très éloigné d'echo, d'un côté comme de l'autre, de sorte qu'on ne peut pas se contenter de dire qu'echo en est une bonne approximation. |
.

|
Ci-dessus, foxtrot est au-delà d'echo, ci-dessous, en deçà. |
.

|
Toutefois, il n'est pas forcément nécessaire d'obtenir une grande précision dans le calcul de ce point foxtrot. Pour incurver la courbe de Bézier, l'orientation de la droite ant-foxtrot joue un rôle plus important que la distance entre ces deux points. On va donc pouvoir tolérer un certain manque de précision dans le calcul de cette distance. |